Have you ever wondered how mathematicians pin down the behavior of functions at specific points? The answer lies in the concept of limits, one of the most fundamental tools in calculus. While a limit generally captures the function’s behavior as input values get infinitely close to a particular point, things become more interesting when we consider the approach from a specific direction. Enter the concept of left and right-hand limits – these tools allow us to examine function behavior from the left and right sides of a point, revealing finer details about the function’s movement.
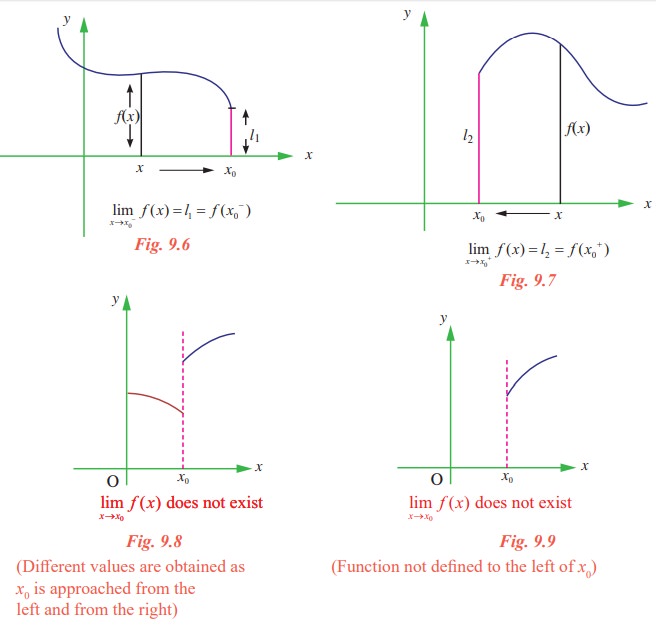
Image: www.brainkart.com
Understanding left and right-hand limits is crucial for several reasons. First, it helps us grasp the full picture of a function’s behavior at a point, even if the overall limit doesn’t exist. Second, these concepts form the foundation for discussing continuity and differentiability, two core concepts in calculus and analysis. Finally, they play a vital role in various practical applications, such as calculating the rate of change in physical systems or modeling the behavior of financial markets.
Getting Started with Limits: A Quick Recap
What is a Limit?
A limit tells us the value a function approaches as its input value gets closer and closer to a specific point. Mathematically, we can represent this idea as follows:
limx→c f(x) = L
This statement indicates that as x gets infinitely close to c, the function f(x) gets infinitely close to the value L. This does not necessarily mean that at x = c, the function equals L. It just tells us the behavior of the function as the input value gets arbitrarily close to c.
The Need for Left and Right-Hand Limits
While the “regular” limit describes the overall behavior of a function, consider a scenario where the function behaves differently as you approach a point from the left versus approaching from the right. In such cases, the regular limit may not exist. This is where the left and right-hand limits come in.
The left-hand limit looks at how the function behaves as x approaches c from values less than c. Similarly, the right-hand limit considers the function’s behavior as x approaches c from values greater than c.
We use specific notations to represent these limits:
Left-hand limit: limx→c– f(x) = L1
Right-hand limit: limx→c+ f(x) = L2

Image: www.chegg.com
Understanding Left and Right-Hand Limits with Examples
Example 1: A Simple Jump Discontinuity
Imagine a function that jumps from one value to another at a specific point. Let’s say for x values less than 2, our function is f(x) = x + 1, and for x values greater than or equal to 2, our function is f(x) = x – 1. We can represent this function graphically.
Now, let’s examine the limits at x = 2.
Left-hand limit: limx→2– f(x) = 3
As x approaches 2 from the left (values less than 2), the function gets arbitrarily close to 3 (x + 1 approaches 3). Similarly, for the right-hand limit:
Right-hand limit: limx→2+ f(x) = 1
As x approaches 2 from the right (values greater than 2), the function gets arbitrarily close to 1 (x – 1 approaches 1).
In this scenario, the left and right-hand limits are different, and the regular limit doesn’t exist. This indicates a *discontinuity* at the point x = 2 – the function “jumps” from one value to another. This jump discontinuity exemplifies why left and right-hand limits are vital for understanding the complete behavior of a function.
Example 2: A Function with an Asymptote
Consider the function f(x) = 1/x. This function has a vertical asymptote at x = 0. Let’s investigate the limits at x = 0.
As x approaches 0 from the left (negative values), the function f(x) decreases without bound. This means it becomes infinitely negative.
Left-hand limit: limx→0– f(x) = -∞
Similarly, as x approaches 0 from the right (positive values), the function f(x) increases without bound and becomes infinitely positive.
Right-hand limit: limx→0+ f(x) = ∞
In this case, neither the left-hand nor the right-hand limit exists (they approach infinity). However, understanding these limits helps us identify the vertical asymptote and describe the function’s behavior near it.
A Deeper Look: The Importance of Continuity
Left and right-hand limits play a key role in determining whether a function is *continuous* at a specific point. A function is continuous at a point if its value at that point is equal to the limit of the function as the input approaches that point. For continuity to hold, the left and right-hand limits must exist and be equal to each other, and they must also equal the value of the function at the point.
For example, in the previous jump discontinuity example, the function is not continuous at x = 2 because the left and right-hand limits do not match. In contrast, in the function f(x) = 1/x, continuity is not defined at x = 0 due to the existence of the vertical asymptote.
Practical Applications of Left and Right-Hand Limits
Beyond theoretical concepts, left and right-hand limits have numerous practical applications, including:
- Modeling Physical Phenomena: In physics, left and right-hand limits help analyze the behavior of physical systems as they approach a specific state. For instance, when calculating the instantaneous velocity of an object at a particular time, we essentially use the concept of the limit, including the idea of approaching the time from both sides.
- Financial Modeling: Left and right-hand limits can be applied to models of financial markets, to understand the behavior of market prices as they approach certain thresholds or events. For example, a model might use limits to predict the stock price behavior leading up to an earnings announcement.
- Engineering Design: In engineering, limits play a crucial role in understanding and analyzing the behavior of structures and systems. For instance, engineers use limits to determine the maximum load a bridge can withstand or to analyze the stability of an airplane wing.
Left and Right-Hand Limits: The Foundation of Calculus
Left and right-hand limits are essential tools in calculus and analysis. They enable us to delve deeper into the function’s behavior at specific points and understand the finer details of its movement. Understanding these concepts allows us to analyze functions more effectively and apply them in diverse fields.
Downloadable PDF: A Comprehensive Resource for Left and Right-Hand Limits
We have compiled a comprehensive PDF resource that provides detailed explanations, additional examples, and exercises for further practice. This PDF is intended to offer a more in-depth understanding of left and right-hand limits and their applications. You can download it [HERE (Replace [HERE] with the actual link to your PDF file)] to enhance your knowledge and explore these concepts further.
Left And Right-Hand Limits Examples Pdf
https://youtube.com/watch?v=PK28_paHp58
Conclusion
The concept of left and right-hand limits equips us with finer tools for analyzing function behavior, allowing us to understand their intricate movements at specific points. From jump discontinuities to vertical asymptotes, the left and right-hand limits help us uncover these details and gain a more complete picture of function behavior. Understanding these limits forms a vital foundation for delving deeper into calculus and its various applications, enabling us to analyze real-world phenomena with greater precision and understanding. Download our PDF resource to explore these concepts further and strengthen your grasp of limits and their role in mathematics.






